[强化学习]强化学习基本概念

https://www.youtube.com/watch?v=vmkRMvhCW5c&list=PLvOO0btloRnsiqM72G4Uid0UWljikENlU

Station And Action

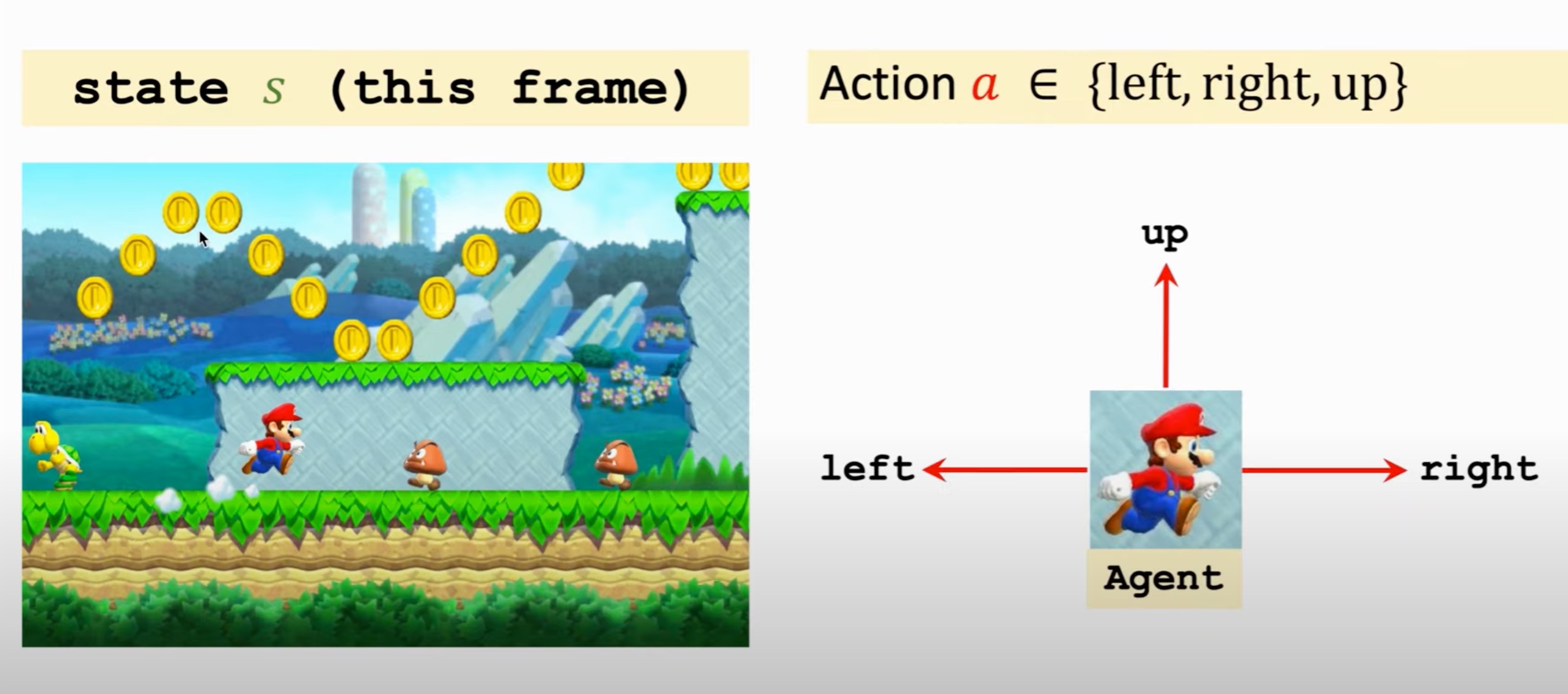
强化学习的主体被称为智能体(agent) 。由谁做动作或决策，谁就是智能体。比如在超级玛丽游戏中，玛丽奥就是智能体。 环境(environment) 是与智能体交互的对象，例如游戏程序就是环境。在每个时刻，环境有一个 状态 (state) ，可以理解为对当前时刻环境的概括。例如当前的游戏画面。而马里奥根据当前游戏画面所做的判断就被称为 动作(Action) 。
策略(Policy) 记为π，策略函数π:(a|s)指的是在状态s的情况下做出动作a的概率。Agent做出一个动作后会得到一个 奖励(Reward) R。并且会得到一个新的状态s+1，这个过程被称为状态转移。状态转移可以是随机的也可以是确定的，一般是随机的。我们用 状态转移概率函数(state transition probability function) 来描述状态转移，记为

$$p_t(s^{\mathrm{\prime }}\mid s,a)=\mathbb{P}(S_{t+1}^{\mathrm{\prime }}=s^{\mathrm{\prime }}\mid S_t=s,A_t=a)$$

状态空间(Station Spae) 是指所有可能存在状态的集合。

环境与智能体的交互过程

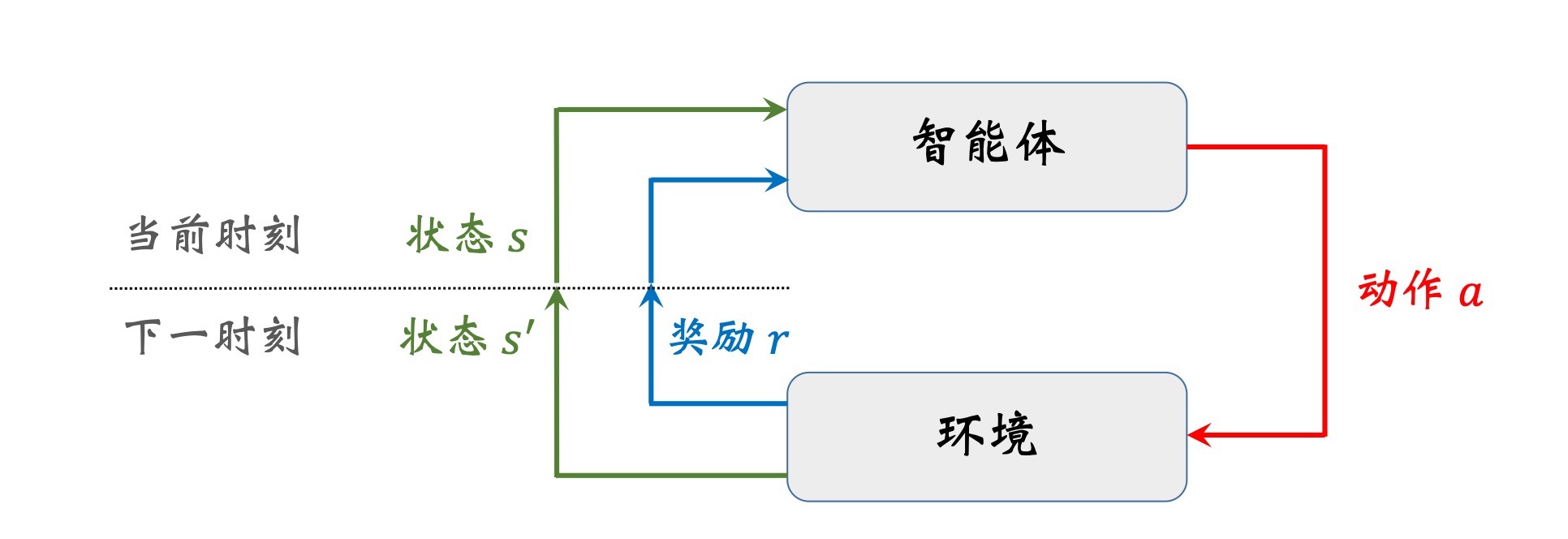
RL中随机性的来源有 动作随机性 和 状态转移随机性

过程：
Observe a frame(state s1)
->make Action a1
->observe a new frame(state s2)
->make Action a2
…

(state,action,reward)trajectory:
s1,a1,r1,…,sT,aT,rT

Reward And Retuen

Return:把t时刻以及后面的奖励全部加起来，就得到了Return

由于t时刻的动作对后面的影响越来越小，所以后面的奖励会乘上一个 折扣率(discounted) $\gamma $

$$U_t=R_t+\gamma \cdot R_{t+1}+{\gamma }^2\cdot R_{t+2}+{\gamma }^3\cdot R_{t+3}+\cdots$$

Value Function

动作价值函数$Q_π(s,a)$，最优动作函数$Q_*(s,a)$,状态价值函数$V_π(s)$都是汇报的期望。

动作价值函数

简单的说，动作价值函数就是在状态s的情况下做出动作a的预估回报，依赖于当前的状态s,动作a以及策略函数π。

当消除了策略函数π的影响，即选择最优策略的时候，就成了最优动作价值函数$Q_*(s,a)$

$$Q_{\star }(s_t,a_t)=\underset{\pi }{max}{Q}_{\pi }(s_t,a_t),\mathrm{\forall }{s}_t\in \mathcal{S},a_t\in \mathcal{A}.$$

状态价值函数

状态价值函数则是用来评估当前状态的好坏。举个例子：
假设 AI 用策略函数 π 下围棋。AI 想知道当前状态 st(即棋盘上的格局)是否对自 己有利，以及自己和对手的胜算各有多大。该用什么来量化双方的胜算呢?答案是状态 价值函数(state-value function):

$$\begin{array}{rl}{V}_{\pi }\left(s_t\right)& ={\mathbb{E}}_{A_t\sim \pi (\cdot \mid s_t)}\left[Q_{\pi }(s_t,A_t)\right]\\ & =\sum _{a\in \mathcal{A}}\pi (a\mid s_t)\cdot Q_{\pi }(s_t,a)\end{array}$$

简单的说，状态价值函数消除了动作对状态的影响，只依赖于策略π和当前的状态s。

---

强化学习的类型

不理解环境(Model-Free RL)

智能体只能一步一步的参与行动并等待反馈，然后再根据反馈参与参与下一次的行动。

理解环境(Model-Base Rl)

智能体能通过想象与判断接下来要发生的情况，并根据想象选择接下来发生情况最好的。

基于概率(Policy-Base RL)

通过分析当前所处的环境，输出采取各种下一步行动的概率，并随机选择其中一个，也就是说所有的行动都有可能被选到，只是可能性不同。常使用的方法有Policy Gradient。

基于价值（Value_Base RL）

智能体选择价值最高的行动。但对于基于连续的动作不能使用这种方法。常用的方法有Q- Learning，Sarsa。

Actor- Critic

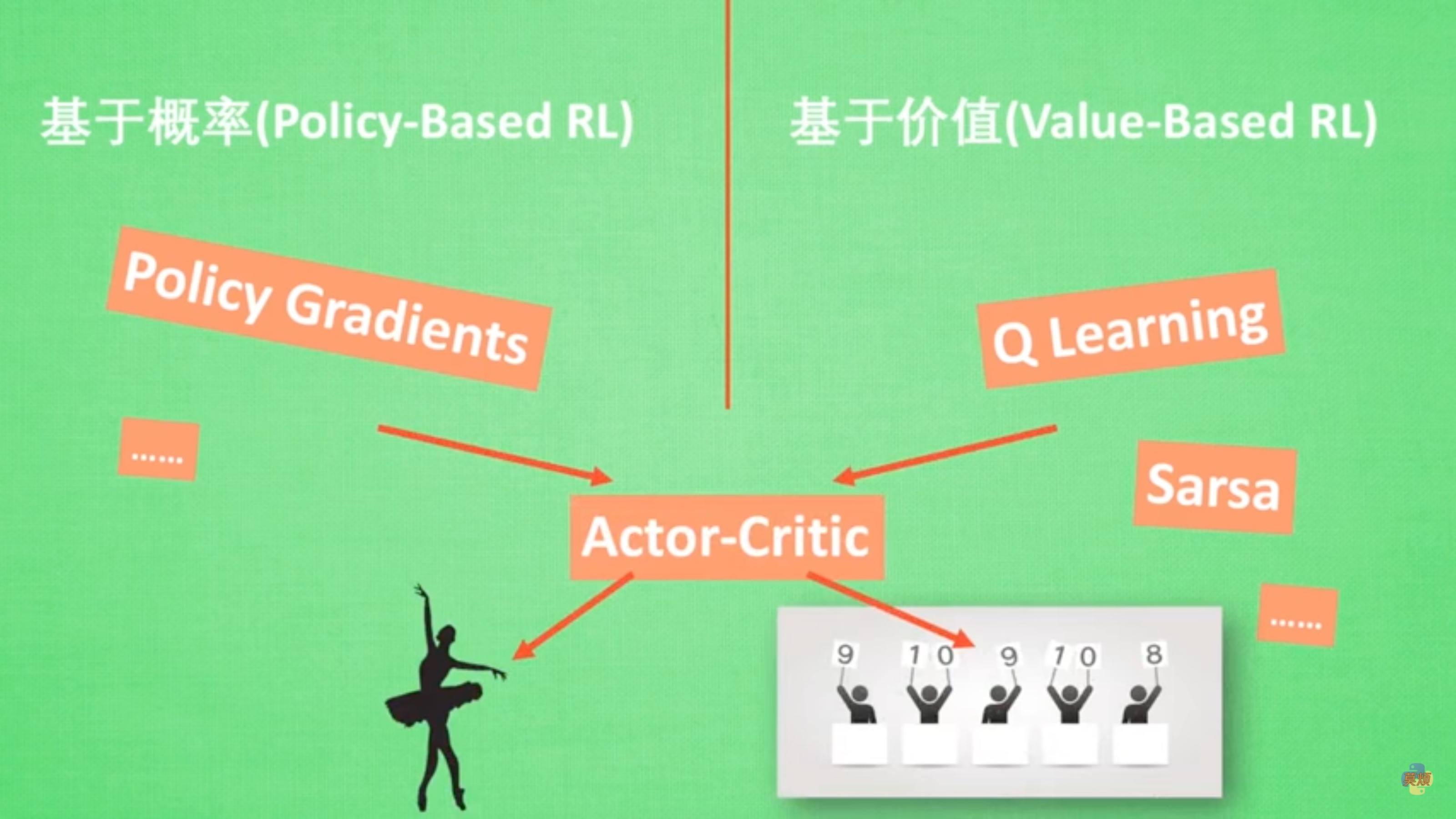
结合基于概率和基于价值的方法。Actor会基于概率做出动作，Critic会基于价值对做出的动作给出价值。加速了学习过程。

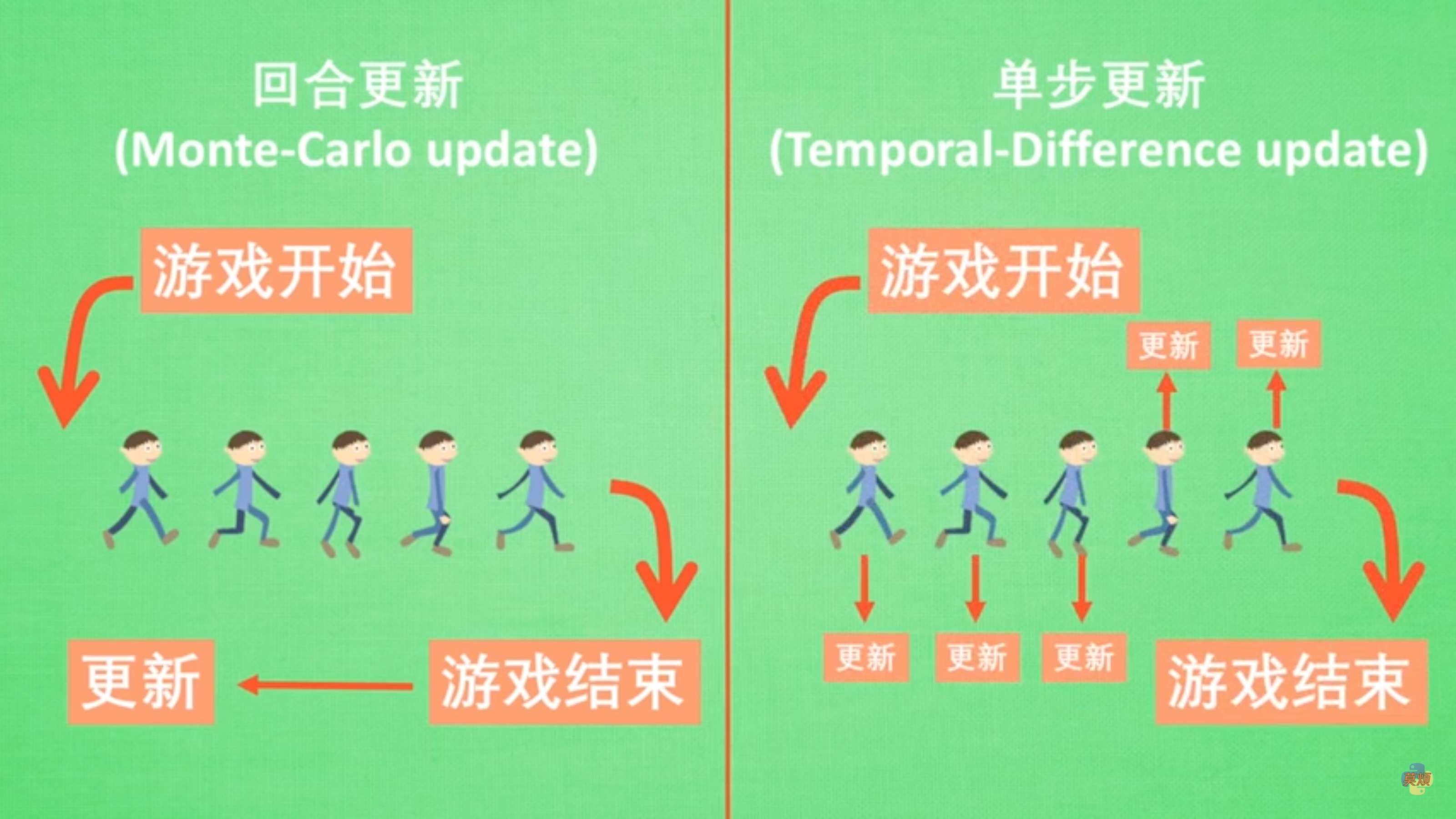
回合更新

每一轮结束后再进行参数的更新。

单步更新

在有学习进行的每一步都在更新。

Actor- Critic

Actor会基于概率做出动作，Critic会基于价值对做出的动作给出价值。

策略网络 π(a|s; θ) 相当于演员，它基于状态s做出动作a。价值网络 q(s, a; w) 相当于评委，它给演员的表现打分，评价在状态s的情况下做出动作a的好坏程度。

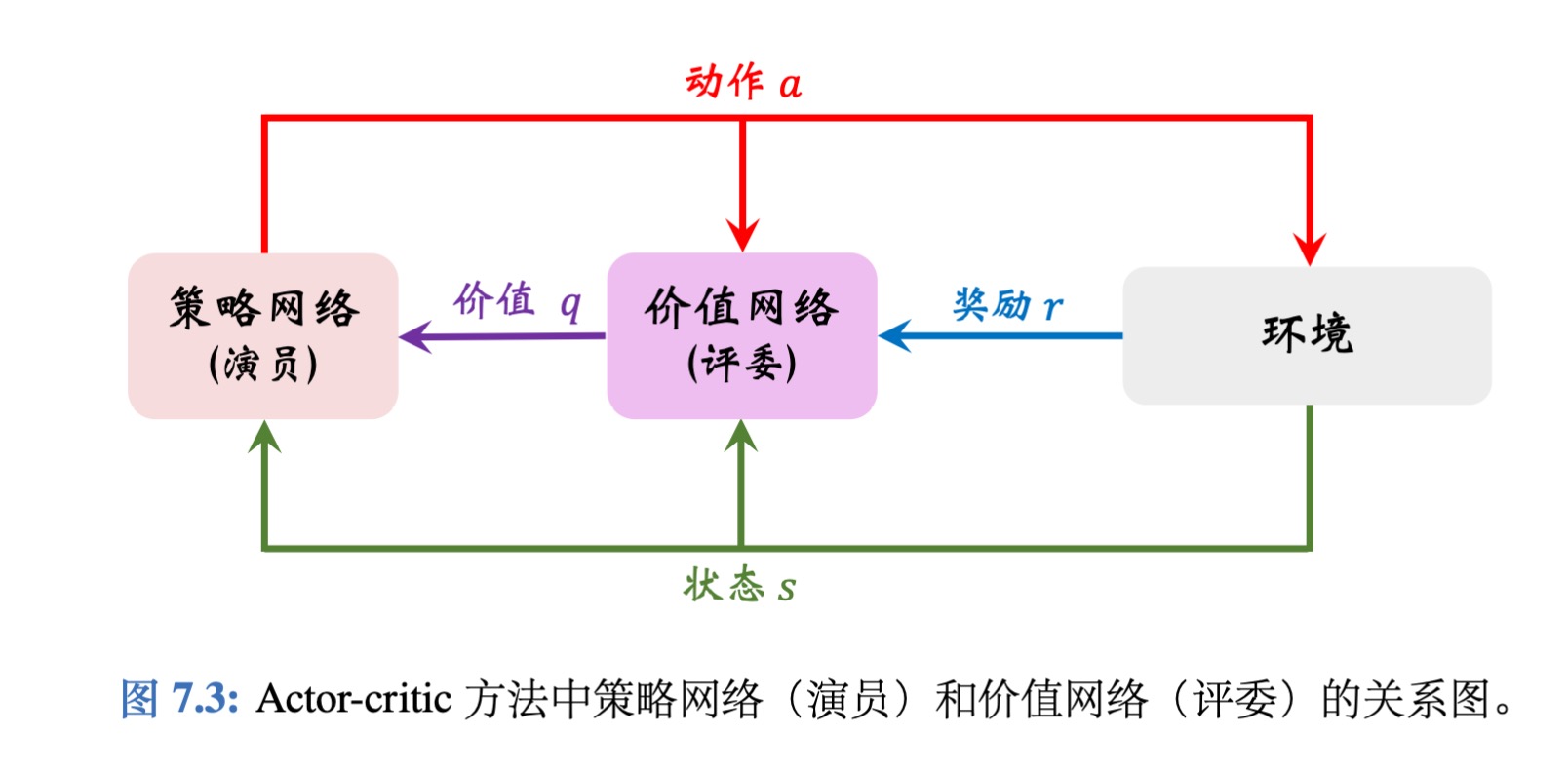
为什么不直接把奖励R反馈给策略网络（演员），而要用价值网络（评委）这样一个中介呢？

• 策略学习的目标函数J(θ)是回报U的期望，而不是奖励R的期望；注意回报U和奖励R的区别。虽然能观测到当前的奖励R，但是它对策略网络是毫无意义的；训练策略网络（演员）需要的是回报U,而不是奖励R。价值网络(评委)能够估算出回报U的期望，因此能帮助训练策略网络(演员)。

训练过程:设当前策略网络参数是$θ_{now}$，价值网络参数是$w_{now}$。执行下面的步骤，将参数更新成$θ_{new}$和$w_{new}$

• 观测到当前状态$s_t$，根据策略网络做决策：$a_t∼π(·|s_t;θ_{now})$，并让智能体执行动$a_t$。
• 根据策略网络做决策：$ \tilde{a_{t+1}} ∼π(·| s_{t+1} ; θ_{now})$ , 但不让智能体执行动作$\tilde{a}_{t+1}$。
• 让价值网络打分:$${\hat{q}}_t=q(s_t,a_t;{\mathit{w}}_{\text{now }})\text{ 和 }{\hat{q}}_{t+1}=q(s_{t+1},{\tilde{a}}_{t+1};{\mathit{w}}_{\text{now }})$$
• 计算 TD 目标和 TD 误差:$${\hat{y}}_t=r_t+\gamma \cdot {\hat{q}}_{t+1}\text{ 和 }{\delta }_t={\hat{q}}_t-{\hat{y}}_t$$
• 更新价值网络：$${\mathit{w}}_{\text{new }}\leftarrow {\mathit{w}}_{\text{now }}-\alpha \cdot {\delta }_t\cdot {\mathrm{\nabla }}_{\mathit{w}}q(s_t,a_t;{\mathit{w}}_{\text{now }}).$$
• 更新策略网络：$${\mathit{\theta }}_{\text{new }}\leftarrow {\mathit{\theta }}_{\text{now }}+\beta \cdot {\hat{q}}_t\cdot {\mathrm{\nabla }}_{\mathit{\theta }}\ln \pi (a_t\mid s_t;{\mathit{\theta }}_{\text{now }})$$

更新价值网络q

• 计算$q(s_t,a_t;w_t)$和$(s_{t+1},a_{t+1};w_t)$
• TD target:$y_t=r_t+\gamma * \max_a $($s_{t+1}$,a_{t+1};$w$)
• Loss:$L(w) = \frac{1}{2}[q(s_t,a_t;w_t) - y_t]^2$
• Gradient descet:$w_{t+1} = w_t - \alpha * \frac{\partial L(w)}{\partial w} |_{w=w_t}$

使用策略梯度算法更新策略网络π

• 让 $\mathbf{g}(a, \boldsymbol{\theta})=\frac{\partial \log \pi(a \mid s, \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \cdot q\left(s_{t}, a ; \mathbf{w}\right)$
• $\frac{\partial V(s;θ,w_t)}{\partial θ}=\mathbb{E}_{A}[\mathbf{g}(A, \boldsymbol{\theta})] $
• 随机抽样一个a根据π(·|$s_t$;θ)。
• 更新梯度：$θ_{t+1} = θ_t + \beta * g(a,θ_t)$